Convertir en binaire
Chargement page et sommaire en cours...
Conversion Décimal vers Binaire
Division décimale : pour la méthode
En divisant un nombre par une base on trouve chaque élément de la base et ici on reconstitue le nombre en base 10, le décimal.Cette méthode est universelle : elle fonctionne dans toutes les bases !
1
2
3
4
Divisons une première fois le nombre par la base,
6587/10 = 658, il nous reste les unités :
7 (poids 0 : 10^0 = unités)
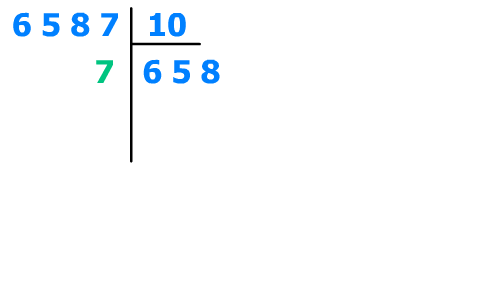
6587/10 = 658, il nous reste les unités :
7 (poids 0 : 10^0 = unités)
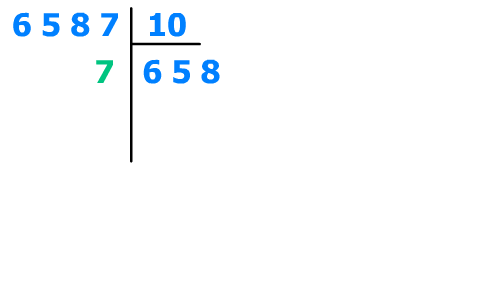
Divisons une seconde fois le nombre par la base,
658/10 = 65, il nous reste les dizaines :
8 (poids 1 : 10^1 = dizaines)
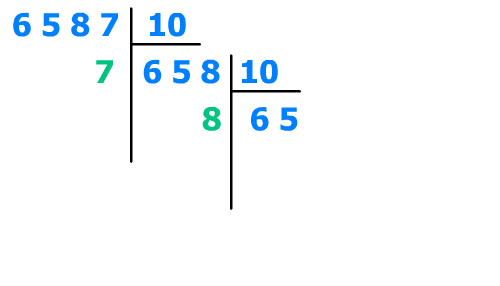
658/10 = 65, il nous reste les dizaines :
8 (poids 1 : 10^1 = dizaines)
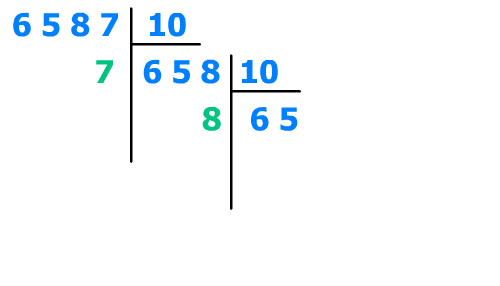
Divisons une troisième fois le nombre par la base,
65/10 = 6, il nous reste les centaines :
5 (poids 2 : 10^2 = centaines)

65/10 = 6, il nous reste les centaines :
5 (poids 2 : 10^2 = centaines)

Enfin le 6 des milliers (poids 3 : 10^3 = milliers) nous restitue un 0 (6/10 = 0) qui n'est pas significatif :
06587 = 6587

06587 = 6587

Conversion par division binaire
Là aussi, nous allons diviser par la base 2 du binaire successivement jusqu'à parvenir à 0...1
2
3
4
5
Divisons une première fois le nombre par la base,
18/2 = 9, il nous reste le bit de poids 0, ici il est nul :
0 (poids 0 : 2^0 = 0)
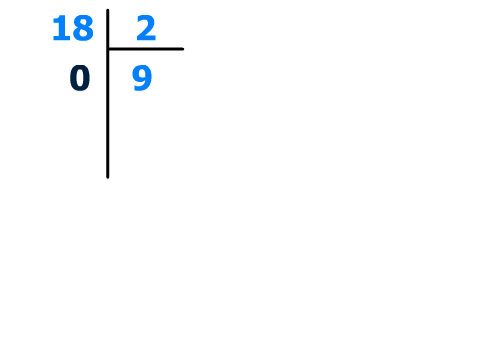
18/2 = 9, il nous reste le bit de poids 0, ici il est nul :
0 (poids 0 : 2^0 = 0)
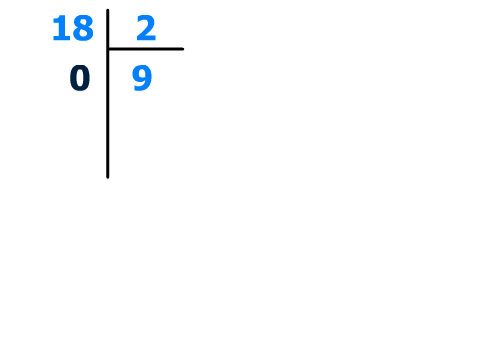
Divisons une deuxième fois le nombre par la base,
9/2 = 4, il nous reste le bit de poids 1, ici il existe :
1 (poids 1 : 2^1 = 2)
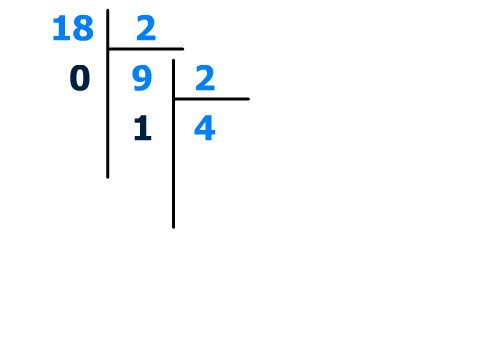
9/2 = 4, il nous reste le bit de poids 1, ici il existe :
1 (poids 1 : 2^1 = 2)
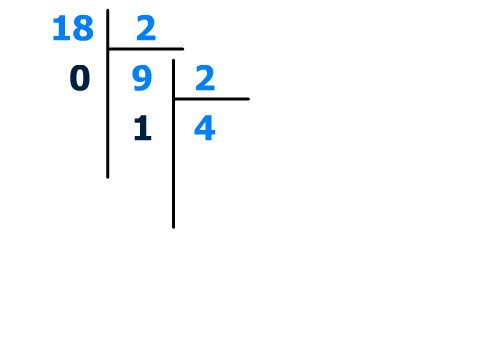
Divisons une troisième fois le nombre par la base,
4/2 = 2, il nous reste le bit de poids 2, ici il est nul :
0 (poids 0 : 2^2 = 4)
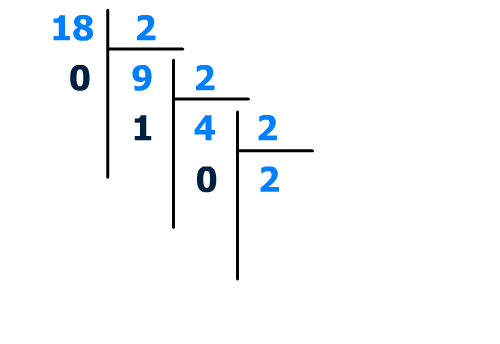
4/2 = 2, il nous reste le bit de poids 2, ici il est nul :
0 (poids 0 : 2^2 = 4)
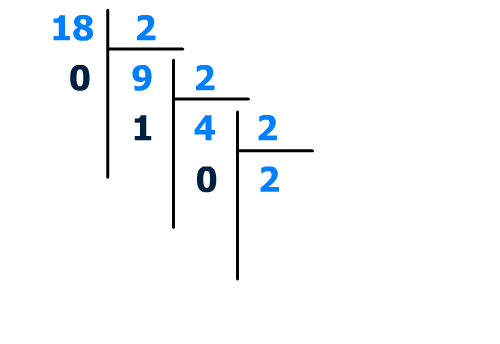
Divisons une nouvelle fois le nombre par la base,
2/2 = 1, il nous reste le bit de poids 3, ici il est nul :
0 (poids 0 : 2^3 = 8)
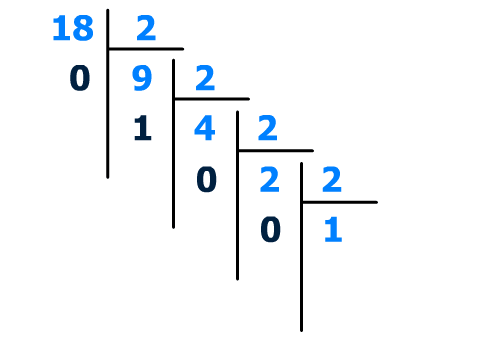
2/2 = 1, il nous reste le bit de poids 3, ici il est nul :
0 (poids 0 : 2^3 = 8)
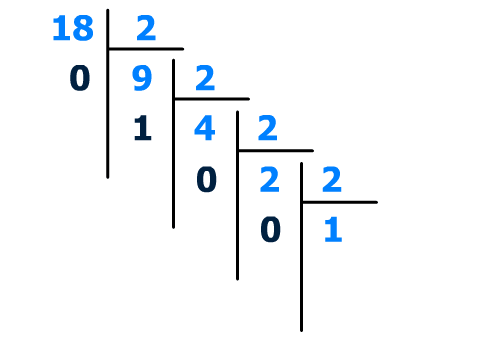
Divisons une dernière fois le nombre par la base,
1/2 = 0, il nous reste le bit de poids 4, ici il existe :
1 (poids 0 : 2^4 = 16)

1/2 = 0, il nous reste le bit de poids 4, ici il existe :
1 (poids 0 : 2^4 = 16)

Méthode intuitive de conversion
Décimal vers binaire par écriture des poids :
On écrit les poids directement de gauche à droite jusqu'à la valeur qui dépasse le décimal à convertir.
Les plus matheux pourront écrire les puissances, sinon il suffit de partir de 1 et de doubler à chaque fois comme sur l'image ci-dessous :

Pour éviter toute confusion, on précise la base après la valeur complète, exemple : 11011110(2), cela permet d'éviter de confondre avec 11011110(10) qui est bien supérieur à 222(10) !
Invité, affichez le quiz :

Cours extrait du stage : INDUSTRONIC
Stage : INDUSTRONIC






