Puissances triphasées
Chargement page et sommaire en cours...
Les puissances en triphasé
Puissances en étoile équilibrée
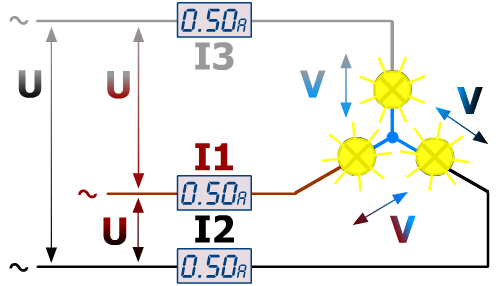
Prenons le cas d'une distribution 230 / 400 :
U = 400 Volts, V = 230 Volts (U / √3)
Chaque ampoule offre une puissance de :
230 V × 0.5 A x 1 Cosφ est ici de 1 : ampoule à filament = résistance pure, aucun déphasage ! = 115 Watt (P = V × I × cosφ)
La puissance totale consommée est de 3 × 115 W= 345 W.
On peut donc écrire qu'en étoile :
P = V × I × 3 × cosφLes 3 lampes recevant V, étant traversées par I, il convient de prendre V, I et de multiplier par 3 et cosφ !
On peut aussi remplacer V par U à condition de le diviser par √3 :
P = (U/√3) × I × 3 × cosφ
Par commodité, on divisera plutôt le 3 (pour les 3 phases) par √3 :
P = U × I × (3/√3) × cosφ ; qui donnera aussi :
P = U × I × √3 × cosφ
Puissances en triangle équilibré
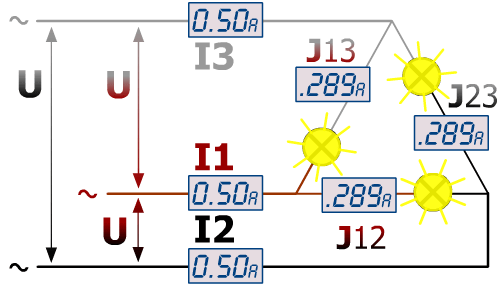
Là encore en 400 V triphasé
Chaque ampoule, reçoit U = 400 V pour une puissance de :
400 × 0.289 × 1 = 115 Watt
Là aussi P total = 3 × 115 W = 345 W.
En triangle on peut écrire :
P = U × J × 3 × cosφLes 3 lampes recevant U, étant traversées par J, il convient de prendre U, J et de multiplier par 3 et cosφ !
Là aussi, remplaçons J par I en le divisant par √3 :
P = U × (I/√3) × cosφ
A nouveau, on divise le 3 du nombre de lampes :
P = U × I × (3/√3) × cosφ ; et donc :
P = U × I × √3 × cosφ
P = U × I × √3 × cosφ
Cette formule est donc universelle, que le montage triphasé soit en étoile ou en triangle, peu importe.On calcule avec les valeurs U et I :
(J est à l'intérieur d'un récepteur triphasé et donc difficile à mesurer par exmple dans les enroulements d'un moteur !).
Le fait de multiplier le résultat d'une phase par √3 au lieu de 3 corrige l'erreur qui consiste à ne pas choisir V ou J tout en assurant la relative universalité de cette formule...
Universalité limitée aux cas pour lesquels I est identique dans les 3 phases, bien naturellement !
Attention !
Comme nous allons le confirmer, la formule P = U × I × √3 × cosφ ne fonctionne qu'avec des récepteurs équilibrés !En résumé :
Pour les montages triphasés équilibrés
Puissance active (W) : P = U × I × √3 × cosφ
Puissance apparenteAttention, c'est le terme employé mais cette puissance n'est point fictive ! C'est celle que doit fournir le générateur et que les câbles doivent transporter ! (VA) : S = U × I × √3
Puissance réactive (VAR) : Q = U × I × √3 × sinφ
Pour les montages triphasés équilibrés
P en Watt indique la puissance 'active' : c'est à dire la puissance réellement convertie (ex : mécanique pour un moteur)
S en VAVolt Ampère, produit direct de U et I sans cosφ la puissance 'apparente' : la puissance fournie et transportée, elle sert à dimensionner générateur, transformateur, protections, sections de conducteurs...
Q en VARVolt Ampère Réactif puissance 'réactive' : cette puissance n'existe que dans les circuits inductifs et capacitifs. En inductif, c'est elle qui crée le champ magnétique tournant, on peut la compenser avec des condensateursVoir cours sur le redressement du cosinus φ ou s'en affranchir avec des variateurs convertisseurs de fréquenceL'utilisation de variateurs, de par leur électronique convertissant le triphasé en continu et recréant du triphasé à partir de 3 onduleurs, s'affranchit du déphasage..
S² = P² + Q²Voir Pythagore en fin de ce cours et donc : S = √(P²+Q²) ou encore P = √(S²–Q²)
Puissances en étoile déséquilibrée
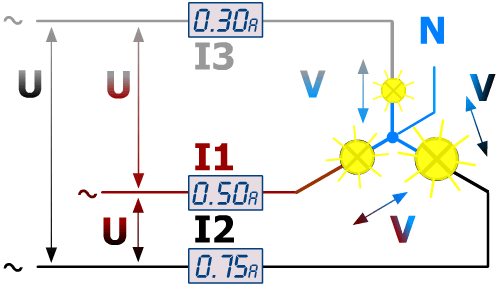
Désormais il est impossible d'appliquer la formule précédente puisque les 3 intensités I ne sont plus identiques...
La solution consiste à effectuer le calcul phase par phase et d'additionner les puissances actives et réactives, pour les apparentes, ce sera un peu différent, déphasage oblige !
P total = (V × I1 × cosφ1) + (V × I2 × cosφ2) + (V × I3 × cosφ3)
Q total = (V × I1 × sinφ1) + (V × I2 × sinφ2) + (V × I3 × sinφ3)
(S total)² = (P total)² + (Q total)² et donc :
S total = √ [(P total²)-(Q total²)]
Q total = (V × I1 × sinφ1) + (V × I2 × sinφ2) + (V × I3 × sinφ3)
(S total)² = (P total)² + (Q total)² et donc :
S total = √ [(P total²)-(Q total²)]
Puissances en triangle déséquilibré
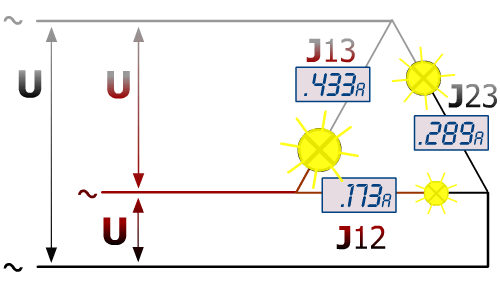
Là aussi il est impossible d'appliquer la formule générale puisque les 3 J ne sont pas identiques...
A nouveau, il conviendra d'effectuer le calcul phase par phase et d'additionner les puissances actives et réactives, pour les apparentes, à nouveau, le triangle de Pythagore :
P total = (U × J1 × cosφ1) + (U × J2 × cosφ2) + (U × J3 × cosφ3)
Q total = (U × J1 × sinφ1) + (U × J2 × sinφ2) + (U × J3 × sinφ3)
(S total)² = (P total)² + (Q total)² et donc :
S total = √ [(P total²)-(Q total²)]
Q total = (U × J1 × sinφ1) + (U × J2 × sinφ2) + (U × J3 × sinφ3)
(S total)² = (P total)² + (Q total)² et donc :
S total = √ [(P total²)-(Q total²)]
Puissances en triphasé déséquilibré !
Voici le récapitulatif des puissances en montage non équilibré, qui est par définition systématiquement le cas dès que l'on utilise au moins un récepteur monophasé, donc à peu près partout !Puissances en triphasé non équilibré (étoile ou triangle)
Puissance active totale en W :
P total = P1 + P2 + P3 = (V × I × cosφ1) + (V × I2 × cosφ2) + (V × I3 × cosφ3)
Puissance réactive totale Q en VAR :
Q total = Q1 + Q2 + Q3 = (V × I × sinφ1) + (V × I2 × sinφ2) + (V × I3 × sinφ3)
Puissance apparente (fournie et transportée) totale en VA :
(S total)² = (P total)² + (Q total)² et donc S total = √ [(P total²)-(Q total²)]
Puissance active totale en W :
P total = P1 + P2 + P3 = (V × I × cosφ1) + (V × I2 × cosφ2) + (V × I3 × cosφ3)
Puissance réactive totale Q en VAR :
Q total = Q1 + Q2 + Q3 = (V × I × sinφ1) + (V × I2 × sinφ2) + (V × I3 × sinφ3)
Puissance apparente (fournie et transportée) totale en VA :
(S total)² = (P total)² + (Q total)² et donc S total = √ [(P total²)-(Q total²)]
Invité, affichez le quiz :

Cours extrait des stages : INDUSELEC & HABPROELEC
Stage : INDUSELEC






