Couplage étoile triphasé

Sommaire de ce cours :

Chargement page et sommaire en cours...

Montage étoile équilibré et déséquilibré

Vidéo sur la triphasé équilibré ou non : analogie mécanique !

Dans cette vidéo, avec une maquette pédagogique équipée de ressorts mécaniques nous réalisons une analogie pour expliquer le point d'équilibre du neutre en étoile triphasé !
Cette analogie permet de comprendre aisément pourquoi les tensions peuvent devenir dangereuses sur un réseau électrique en cas de rupture du neutreTel les ressorts qui s'allongent, les tensions vont augmenter de manière incontrôlée si le neutre (clou central) n'est plus présent car coupé ! !

Schéma des tensions :

Schéma des tensions tel qu'en début de vidéo : à l'équilibre.
Le fil de neutre est représenté en pointillés, car il est inutile, aucune tension n'existant entre neutres artificiel et réel, l'intensité sera forcément nulle (I = 0 / R) comme le rappelle la représentation des ressorts à droite !
Montage étoile équilibré

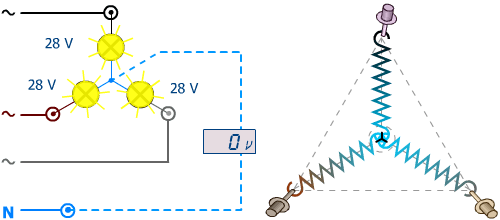
Etoile équilibrée :

U = V × √3

A l'équilibre, le neutre n'est pas indispensable, il se récrée seul :
On le nomme le neutre artificiel !

Démonstration dans les conseils+ U V racine de 3 en fin de page.

Animation sur le montage étoile

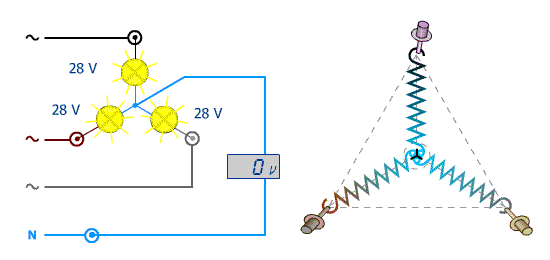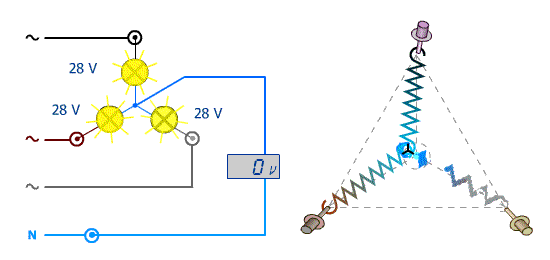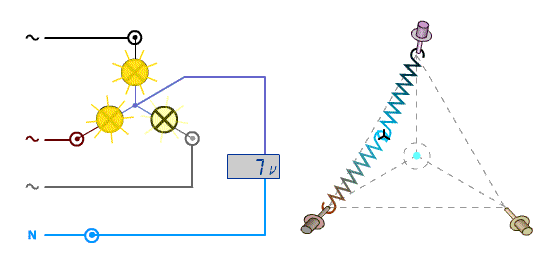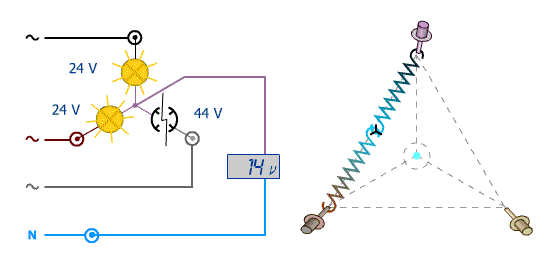
Cliquez l'image pour relancer l'animation

Ci-dessous le déséquilibre des tensions (équivalence distance par analogie).
A gauche comme dans notre exemple en 28 / 48 Volts, à droite les valeurs que l'on aurait sur un réseau classique 230 / 400 V.
Notez que l’ampoule grillée verrait un potentiel de 230 + 115 = 345 V à ses bornes !
Mesure étoile déséquilibre

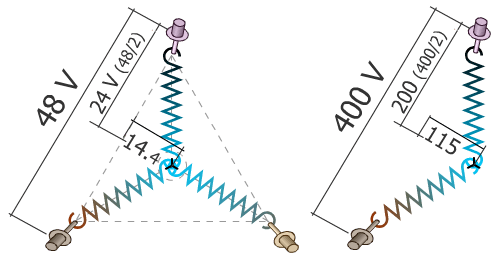
Détail des tensions

Rappel : U = tension composée entre phases
V = tension simple entre phase et neutre.
U = V x √3 (voir conseils+ en fin de cours)

Il reste 2 lampes identiques, L1 et L2, en série entre 2 phases.
La tension à leurs bornes est de U/2 ; VL1 = VL2 = 48 / 2 = 24 V
Calculs tensions étoile

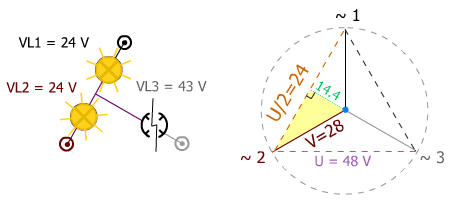
Considérons le triangle rectangle jaune, son hypoténuse est V et vaut 28 V.
On peut appliquer Pythagore puisqu'un second coté est connu : 48 / 2 = 24 V.
Ainsi, le coté en vert = √(28² - 24²) = √(784 - 576) = √208 = 14.4 V
La tension aux bornes de la lampe grillée L3 = coté vert + V.
Donc L3 = 14.4 + 28 V ; L3 = 42.4 Volts (43 V vus sur la vidéo !).

Ici le montage est bien déséquilibré avec présence de surtensions dues à la rupture du neutre !