Prérequis, Conseils+ et cours Connexes
Chargement page et sommaire en cours...
Pythagore
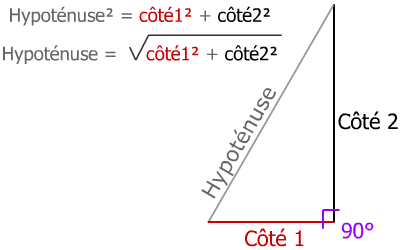
Le carré de l’hypoténuseCôté le plus long est égal à la somme des carrés des 2 autres cotés.
hypoténuse² = côté 1² + côté 2² et donc :
hypoténuse = √(côté 1² + côté 2²)
Voilà le théorème de Pythagore, il ne s'applique qu'aux triangles rectanglesTriangles qui possèdent un angle droit à 90°.
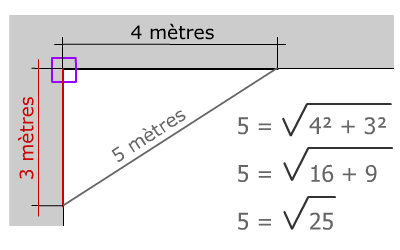
Les maçons l'utilisent bien souvent avec le fameux "3 ; 4 ; 5"Pour vérifier que 2 murs sont bien à l'équerre, et forment donc un angle droit, il suffit de pointer 3 mètres sur un mur, 4 mètres sur l'autre et de mesurer la distance entre les 2 points. Elle doit être de 5 mètres ! Cela fonctionne avec "3 ; 4 ; 5" ou "1.5 ; 2 ; 2.5" et tout multiple de ces 3 valeurs ! !
Rapport entre U et V en triphasé
1
2
3
4
5
6
7

La somme vectorielle U des 2 tensions identiques déphasées de 120° est V × √3. La série de 7 images ci-dessous, nous permet de comprendre l'origine de ce rapport.
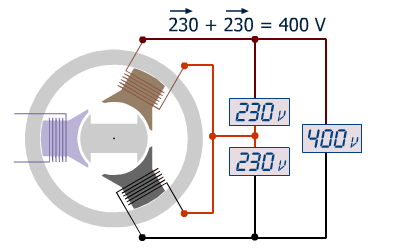
La tension composée U forme un triangle dont chaque branche (U) est la somme vectorielle de 2 tensions simples V.
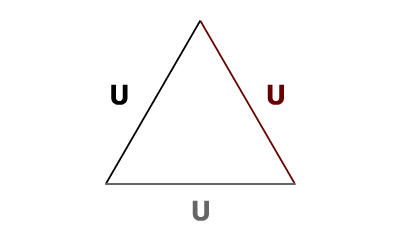
Lorsqu'une tension simple V est maxi, l'autre ne l'est pas et par moment elles sont tout simplement inversées ! Il convient de faire une addition vectorielle en tenant compte du déphasage de 120° ! Commençons par représenter les 3 tensions composées U...
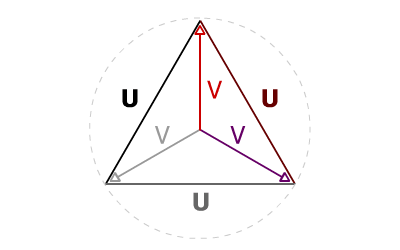
Les tensions composées U forment un triangle équilatéralEquilatéral : 3 cotés égaux
Isocèle : 2 cotés égaux.. Les tensions simples J se rejoignent au centre du triangle équilatéral nous offrant 3 triangles isocèlesEquilatéral : 3 cotés égaux
Isocèle : 2 cotés égaux.. On notera que le centre du triangle équilatéral évoque le neutre, chaque pointe une phase.
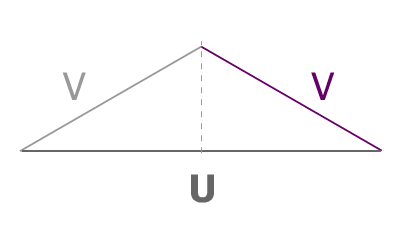
Ne conservons qu'un triangle isocèle, le rapport entre V et U étant le même pour les 3. Nous constatons bien avec ce schéma que la tension U est constituée de V↗ plus V↗
Traçons une perpendiculaire à U passant par le point de jonction entre les 2 V : le sommet.
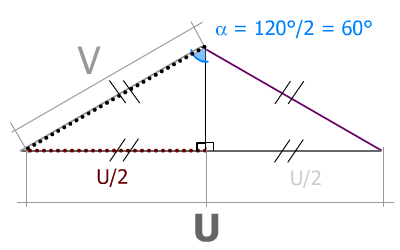
Nous observons des symétries dont nous connaissons tous les angles : α = 120° / 2
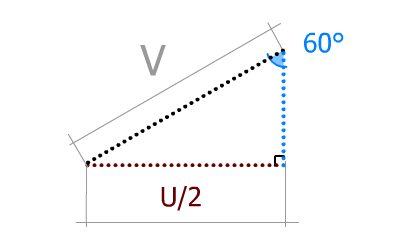
V est l'hypothénuse de notre triangle rectangle.
sinα = opposé / hypothénuse ; donc sinα = (U / 2) / V
Si l'on cherche U on écrira : U / 2 = V × sinα
Et donc U = V × 2 × sinα et 2 × sin60° = 1,732
1.732² = 3 donc U = V × √3
Somme des intensités en triphasé
Récepteur équilibré
Montage triangle ou étoile sans neutre
La sommeN'oublions pas que nous devons effectuer une somme vectorielle instantanée ! des intensités dans les phases est toujours égale à 0. Tout ce qui rentre doit ressortir !
Si tel n'est pas le cas, le seul chemin possible est celui du défaut : le fil de PEProtection électrique via la masse !
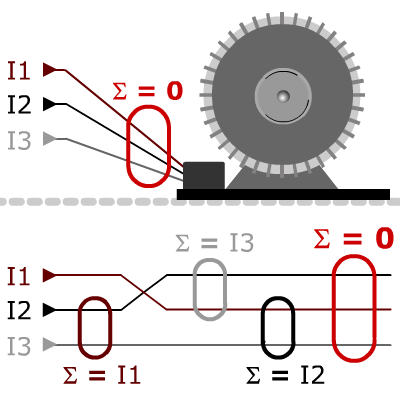
CI-dessus les sommes de 2 intensités. La somme de 2 intensités de phase est toujours identique à la phase restante.
Celà vous semble étrange ? Pensez que l'on raisonne toujours en somme vectorielleExemple avec 1 A : I1 = I2 = I3 = 1 A
Donc 1 A↗ plus 1 A↗ = 1 A !
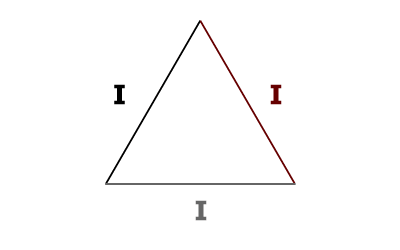
Remplacez les côtés du triangle équilatéral ci-dessus par les vecteurs d'intensités... !
Récepteur en étoile non équilibré
Montage étoile avec neutre
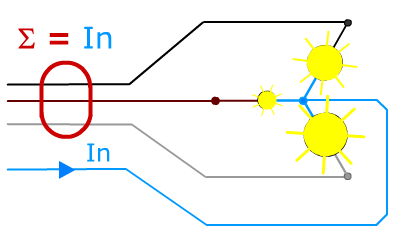
La somme vectorielle des intensités dans les phases est égale à l'intensité du courant dans le neutre.
Rapport entre I et J en triphasé
1
2
3
4
5
6
7

La somme vectorielle I de 2 intensités identiques déphasées de 120° est J × √3. La série de 7 images ci-dessous, nous permet de comprendre l'origine de ce rapport.
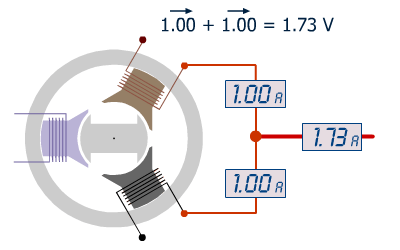
L'intensité I est l'intensité des phases et résulte en triangle de la somme vectorielle de 2 intensités J.

Lorsqu'une intensité J est maxi, l'autre ne l'est pas et par moment elles sont tout simplement inversées ! Il convient de faire une addition vectorielle en tenant compte du déphasage de 120° ! Commençons par représenter les 3 intensités I...
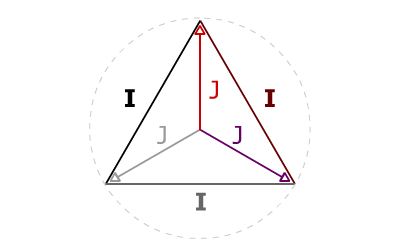
Les intensités I forment un triangle équilatéralEquilatéral : 3 cotés égaux
Isocèle : 2 cotés égaux.. Les intensités J se rejoignent au centre du triangle équilatéral nous offrant 3 triangles isocèlesEquilatéral : 3 cotés égaux
Isocèle : 2 cotés égaux.. On notera que le centre du triangle équilatéral évoque le neutre, chaque pointe une phase.
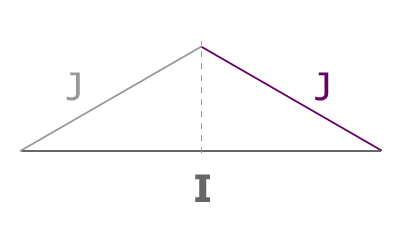
Ne conservons qu'un triangle, le rapport entre J et I étant le même pour les 3. Nous constatons bien avec ce schéma que l'intensité I est constituée de J↗ plus J↗
Traçons une perpendiculaire à I passant par le point de jonction entre les 2 J : le sommet.
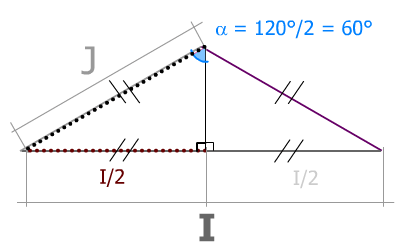
Nous observons des symétries dont nous connaissons tous les angles : α = 120° / 2
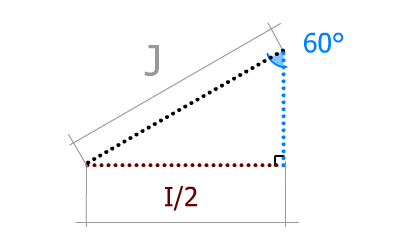
J est l'hypothénuse de notre triangle rectangle.
sinα = opposé / hypothénuse ; donc sinα = (I / 2) / J
Si l'on cherche I on écrira : I / 2 = J × sinα
Et donc I = J × 2 × sinα et 2 × sin60° = 1,732
1.732² = 3 donc I = J × √3
Cours connexes recommandés par l'auteur :
Cours extrait des stages : INDUSELEC & HABPROELEC
Stage : INDUSELEC






