D'où provient le déphasage ?
Chargement page et sommaire en cours...
Pourquoi le déphasage ?
Le cas du récepteur résistif
Toute résistance C'est le terme usuel mais on devrait utiliser : résistor ou résisteur. Dans tous les cas il s'agit d'un dipôle ; composant à 2 pattes dont la seule fonction est de chauffer !pure :- Ampoule à filament
- Résistance chauffante (four, lave vaisselle ou linge, convecteur, fer à repasser, fer à souder...)
- Composant électronique :

Modifient tension et intensité en les convertissant en chaleurNon perceptible en général :-)...
Pour ces récepteurs électriques, le sens du courant n'a aucune influence. Leur inertie est telle que la fréquencePour qu'une ampoule clignote, il faudrait une fréquence < à 24 Hz, pour qu'un convecteur électrique fasse varier, de manière perceptible, la température d'une pièce ; il faudrait une fréquence comptée en minute et non pas par seconde au vu de l'inertie thermique ! n'a aucune incidence non plus... Ainsi aucun déphasage n'existe dans leur cas. On peut donc utiliser la formule, P = U × I, issue du courant continu !
La 'résistance' se comporte de manière indifférente en alternatif et en continu !
Et notre bobine (solénoïde) ?
Là, tout se complique ! Souvenez-vous : toute variation de champ (et donc flux) magnétique engendre une tension induite ! Soyons logique : le courant alternatif sinusoïdal provoque en permanence une variation de champ induit dans une bobine par le fameux effet de selfSelf-induction, auto induction d'une bobine due à son inductance propre... !Ainsi, la bobine va s'opposer en permanence à ce courant en devenant générateur avec 2 conséquences que l'on va vérifier en expériences vidéo et valider en animations pédagogiques :
- La 'résistanceOn abandonne le terme résistance R pour éviter le confusion entre 2 valeurs différentes (R pour le continu, Z pour l'alternatif) au profit de l'impédance Z !
En effet, le résultat : 'R ou Z' = U / I sera différent en alternatif qu'en continu ; à tension efficace identique il va de soi ! Abandon de R pour : Z = U / I en ~ !' est supérieure, on la nomme : impédance - Un retard va apparaître : il provoque le déphasage !
Vidéo sur le retard issue de l'électromagnétisme disponible en connexes :
La bobine va requérir notre attention et sera responsable d'un 'cos φ' comme le prouve cette vidéo !
Le condensateur, allié dans nos besoins !

Si le condensateur est surtout un composant d’électronicien, il s'avère fort utile aux électrotechniciens !
Il se comporte à l'inverse de la bobine, opposant sa capacitance à l’inductance du solénoïde...
En courant continu :
- Court-circuit franc à la mise sous tension
- Impédance infinie en régime établi, une fois que le condensateur est chargé !
En alternatif :
- Se charge et se décharge en permanence, impédance diminuant avec la fréquencePlus on va le contraindre à se charger, décharger, plus l'intensité circulera...
- De part cette caractéristique, il introduit lui aussi un retard mais de tension !
Appelé scolairement une avance de courant (intensité) ce qui peut gêner : on ne remonte pas le temps !
Un peu plus délicat d'expliquer avant les expériences mais faisons une analogie :
Si vous souhaitez entraîner un volant d'inertie, il vous demandera du couple ou de la force avant tout déplacement, toute variation de vitesse (de tension pour le condensateur) :
On peut aussi le comparer à un accumulateur sans résistance :
- Capable de se charger instantanément, d'où l'intensité très élevée avant que la tension à ses bornes n'augmente (lors de la charge).
- Capable de restituer instantanément (lors de la décharge), lors de la décharge les 2 étant parfaitement symétriques.
Charge et décharge du condensateur, U en retard, I en 'avance'
Les 2 ampoules de la vidéo étant identiques, la symétrie quant aux temps d'allumage démontre que le condensateur restitue tout ce qu'il a emmagasiné sans perte.
Ce sont ces temps de charge et de décharge qui provoquent le retard'Avance' d'intensité... de tension aux bornes du condensateur.
Enfin on notera surtout qu'il se comporte comme un court-circuitLa tension, 24 V, est intégralement aux bornes de l'ampoule lors de la mise sous tension, alors qu'elle est en série avec le condensateur. Progressivement ce dernier se charge :
Uc (condensateur) augmente et la tension Ul (lampe) diminue... à la mise sous tension et comme un isolant en régime établiUne fois que Uc = Ug (générateur), Ul = 0 car I = 0 !
En effet, Ug – Uc = 0 et donc I = 0 / R circuit = 0 ! ! NoteLes plus attentifs auront noté que l'inverseur bascule vers la gauche quand le commun est relié en fait à droite : cela est ainsi, les inverseurs ont un mécanisme inversé en interne, nous n'avons pas voulu tricher en croisant les fils....
Ce sont ces temps de charge et de décharge qui provoquent le retard'Avance' d'intensité... de tension aux bornes du condensateur.
Enfin on notera surtout qu'il se comporte comme un court-circuitLa tension, 24 V, est intégralement aux bornes de l'ampoule lors de la mise sous tension, alors qu'elle est en série avec le condensateur. Progressivement ce dernier se charge :
Uc (condensateur) augmente et la tension Ul (lampe) diminue... à la mise sous tension et comme un isolant en régime établiUne fois que Uc = Ug (générateur), Ul = 0 car I = 0 !
En effet, Ug – Uc = 0 et donc I = 0 / R circuit = 0 ! ! NoteLes plus attentifs auront noté que l'inverseur bascule vers la gauche quand le commun est relié en fait à droite : cela est ainsi, les inverseurs ont un mécanisme inversé en interne, nous n'avons pas voulu tricher en croisant les fils....
Analogie avec la bobine
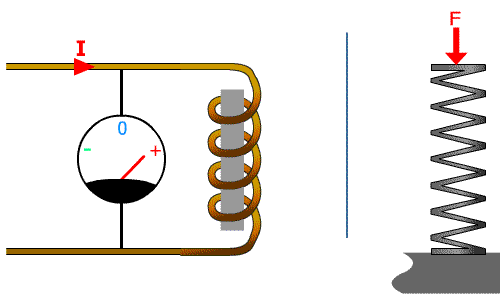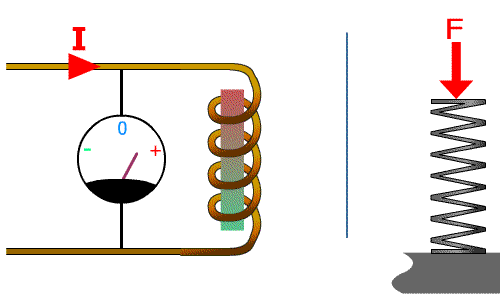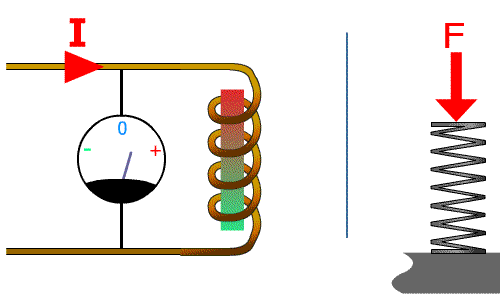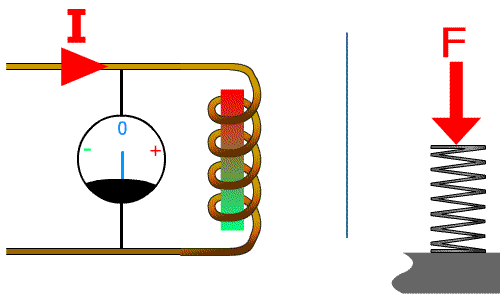
Cliquez pour relancer
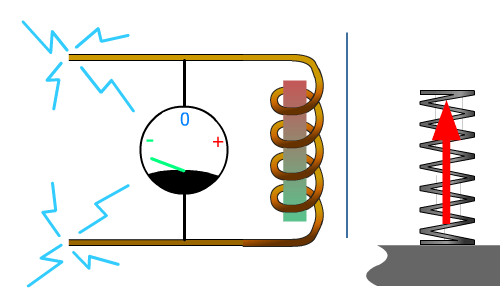
Lorsque l'on applique une tension la bobine de droite, elle s'oppose à ce changement. S'induit à son tour d'une tension opposée ce qui limite fortement l'intensité. Elle crée alors un champ magnétique.
A droite le ressort soumis à un déplacement n'oppose que peu de résistance mécanique au début : la force est faible, il va emmagasiner de l’énergie 'mécanique'En simplifiant : l'énergie emmagasinée sous forme d'énergie cinétique = énergie potentielle mécanique que le lâcher du ressort libérera !.
En régime établi (stabilisé), la bobine se comporte comme un fil, tout comme le ressort ne se comprime plus.
L'illustration ci-dessous précise ce qui se produit lors de la coupure ou rupture brutale :
Coupure alimentation pour la bobine = surtension inverseE = - Δ Φ / Δ t
t tend vers 0 donc E (en Volts) tend vers ∞ l'infini !.
Relâchement de la contrainte sur le ressort = 'sur-vitesse' opposée !
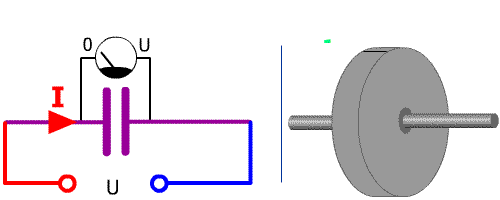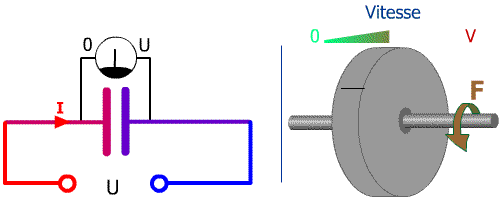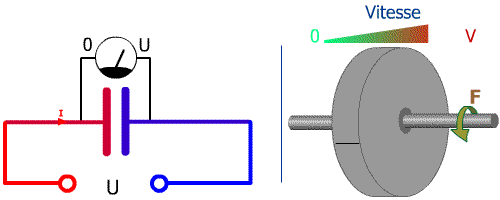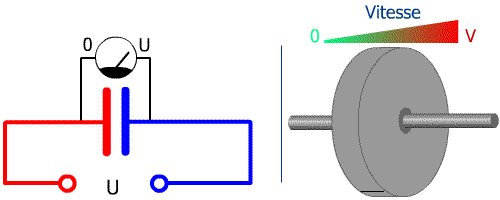
Analogie avec le condensateur
Cliquez pour relancer
En alimentant un condensateur vide, on engendre une forte intensité avant de voir la tension augmenter à ses bornes.
Par là même, en lançant un volant d'inertie à l'arrêt, on fournit un fort couple avant qu'il ne prenne de la vitesse.
Contrairement au couple bobine / ressort qui restitue son énergie dès la déconnexion ; le couple condensateur / volant d'inertie va conserverLe condensateur est en réalité sujet à l'auto-décharge, quelques jours en moyenne. Le volant subira les frottements et ralentira plus rapidement... l'énergie emmagasinée.
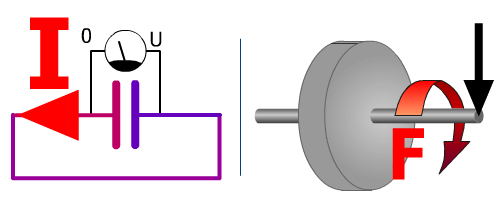
Ci-dessous la restitution brutale en court-circuit pour le condensateur, avec un frein pour le volant :
SurintensitéI = C × U / t
t tend vers 0 donc I tend vers ∞ l'infini pour le condensateur.
Couple très élevé pour le volant...
En résumé le condensateur :
- Ne produira jamaisAttention, le condensateur ne produit jamais de surtension, mais vous pouvez entendre cette erreur : sachez que ce sont les inductances, (incluant l'inductance naturelle des fils), qui provoquent la surtension, le condensateur ne pourra que la stocker, quitte à ce qu'elle le détruise... de surtension
- Peut engendrer une surintensité
- Retarde la variation de tension à ses bornes
La bobine :
- N'engendre jamais de surintensité
- Peut provoquer une surtension
- Retarde les variations d'intensité qui la traversent
Invité, affichez le quiz :

Stage : INITELEC






