Mesures de Z en alternatif : R L C

Sommaire de ce cours :

Chargement page et sommaire en cours...

Impédances Z en alternatif !

Vidéo : le récepteur inductif, la bobine, en alternatif ~

Que retenir de cette vidéo d'observation du comportement d'une bobine inductive en alternatif ?

Notons : 90 Ω (au lieu de 15 Ω en 12 Vcc12 V Courant Continu : alors que la tension est moins de 2 fois supérieure
(en 12 V le relais ne colle pas) l'impédance elle, est 6 fois plus grande !) et ≃ 72° de déphasage électrique !

On constate ainsi que la bobine à cause de son inductance engendre un décalage temporel nommé déphasage électrique qui provoque une valeur d'impédance supérieure à la résistance de la bobine alimentée en courant continu !

Vidéo : le condensateur en alternatif ~

La vidéo nous démontre que le condensateur de 35 µF ≃ 90 Ω à 50 HzDeux en parallèle : 15 + 20 = 35 µF
L'impédance d'un condensateur Z = 1 / (C × ω) avec ω = 2 × Π × f (50 Hz)
1 / (35 × 2 × 3.14 × 50) ≃ 1 / 0.011 ≃ 90 Ω (comme pour la bobine rien à voir avec le CCCourant Continu pour lequel on passait de 0 Ω à ∞) provoque un déphasageLà aussi décalage temporel mais opposé par rapport à l'inductance de la bobine ! d'exactement 90° !

J'ai volontairement choisi d'utiliser 35 µFDeux en parallèle : 15 + 20 = 35 µF
L'impédance d'un condensateur Z = 1 / (C × ω) avec ω = 2 × Π × f est détaillée dans électronique/composants de capacité pour les condensateurs afin d'obtenir la même valeur d'impédanceOn va bientôt voir pourquoi (redressement cos Φ) !
Sinon, le calcul d'impédance de bobines : Z = L × ω est lui aussi abordé dans :
électronique/composants que la bobine : 90 Ω. Nota : lorsque la capacité augmente, l'impédance diminue.

Vidéo : le résistor (résistance) en alternatif ~

Notons dans cette vidéo : 200 Ω pour le résistor (comme en CCCourant Continu) et aucun déphasageC'est pour cela qu'insérer un shunt, résistance faible, en série pour avoir une image de l'intensité ne perturbe pas les résultats !

Une résistance pure, résistor, se comporte à l'identique en courant continu et en courant alternatif :

Impédance identique à la résistance
Aucun déphasage

Récapitulatif des vidéos

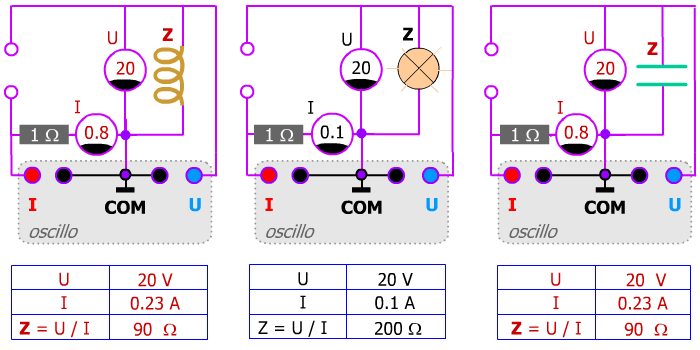
Notes sur le schéma : la résistance de 1 Ω sert de shunt pour voir l'image de l'intensité I dans la voie rouge de l'oscilloscope alors que la bleu affiche la tension dans le récepteur. Pour des raisons de clarté, l'oscilloscope est placé en bas sur le schéma ci-dessus.

Hormis pour notre ampoule purement résistive, les 'impédancesRappel : le nom de résistance ne peut être conservé puisque la valeur change pour la bobine et le condensateur' en alternatif n'ont rien à voir avec les résistances en continu...
Aussi, on nommera les impédances Z et si R est acceptable pour un résistor, il conviendra d'utiliser Z qui précise que l'on travaille en alternatif.

Pourquoi la bobine possède une impédance Z > R sa résistance ?
En courant continu lisse établi, seule la résistance du fil due à sa longueur, son matériau et sa section limitent le passage du courant électrique.
Si l'on déroule la bobinePensez à l'enrouleur électrique ! C'est pour cela qu'au dessus de 1/4 à 1/3 de sa puissance nominale il convient de le dérouler !

il en ira exactement de même en alternatif !
Oui mais elle est enroulée, possède un nombre de spires et s'oppose aux variations en générant un champ magnétique auquel elle se soumet par effet de 'self' auto-induction ce qui induit une tension E qui vient s'opposer et donc se soustraire (de manière vectorielle à cause du déphasage) à l'alimentation, diminuant l'intensité :
I = (U – EU générateur ; E tension induite (ΔΦ / Δt). E est plus faible que U car la bobine agit en récepteur pour devenir générateur, le rendement est inférieur à 100% !) / RLà on prend bien R en continu, c'est le U - E qui diminue le résultat et donne Z :
Z = U / I ; R = (U - E) / I

Récapitulatif, impédance"Résistance" en alternatif et résistanceA réserver au courant continu

Z = U / I ; Z = impédance en ~

Une bobine provoque toujours un déphasage < à 90°Constituée de fil, elle offre toujours une résistance non nulle
R = ρ × lg / S, ce qui empêche un déphasage 'parfait' de 90°
Le déphasage est inexistant pour une résistance pure non bobinéeAttention, un fil résistif enroulé pour formé une résistance présente une inductance non négligeable et donc un déphasage

Un condensateur provoque un déphasage de -90°Dans le sens opposé à l'inductance.
Soit 180° par rapport à l'inductance pure, parfaite (théorique car sans résistance)
Z d'une bobine augmenteZL = L × ω (en négligeant sa résistance) proportionnellement à la fréquence
Z d'un condensateur diminueZC = 1 / (C × ω) proportionnellement à la fréquence

L'impédance réelle d'un récepteur est nommée Z
La réactanceConcerne bobines et condensateurs 'impédance imaginaire parfaite' est nommée X
Le condensateur, considéré parfait, est nommé C avec ZC = XCSon impédance est confondus avec sa réactance puisqu'il ne possède par de résistance et déphase de -90° = 1 / (C × ω)
On termine avec L, le nom de l'inductance parfaite ZL < L × ω, XL = L × ω

Z Bobine = √[RRésistance de la bobine en continu due à son fil :
ρ × (L / S)² × (LInductance de la bobine en Henry
Liée au nombre de pires, à sa longueur, à la présence d'un noyau × ωPulsation : 2 × π × f (Hertz))²]

Z Condensateur = 1 / (CValeur du condensateur en Farad × ωPulsation : 2 × π × f (Hz))