Puissances active, réactive, apparente
Chargement page et sommaire en cours...
Puissances en monophasé
Facteur de puissance, expérience en vidéo
Si l'on reprend les valeurs de puissances vues dans la vidéo :
- Puissance ≃ 1.8 Watts et S ≃ 4.6 Watts
- P / S = 1.8 / 4.6 ≃ 0.4
- Le rapport R / Z était lui ≃ 0.17 pour 0.3 lu à l'oscilloscope, pardonnez l'imprécision...
A la décharge de l'expérience, notre wattmètre n'est pas très précis pour de si faibles valeurs mais le résultat est intéressant puisque dans tous les cas S ≫ P, le ratio est dans tous les cas d'environ 3 !
On démontre ainsi pourquoi le ratio entre P la puissance active en Watt et S la puissance apparente mais fournie et distribuée est aussi appelée facteur de puissance !
Ce que coûte un 'mauvais cosφ'
Le cosinus phi, appelé facteur de puissance, est donc le rapport entre la puissance 'apparente' S en VA / P en W(S en Volt × Ampère) / (P en Watt). C'est pour cela que le cos φ est souvent confondu avec le rendement électrique. C'est incomplet notamment car il existe, comme vu en vidéo, des pertes Joule pour les récepteurs inductifs puisqu'ils comportent tous une résistance intrinsèque (moteurs, transformateurs, ballast de tube fluorescent...). Réprésentation graphique illustrant S ≫ PA prendre comme image, il s'agit d'une simplification illustrative imprécise mais dont le sens est analogue.Pour obtenir des surfaces (puisque P = U × I) équivalentes, on constate que I doit augmenter lorsqu'il existe un déphasage !
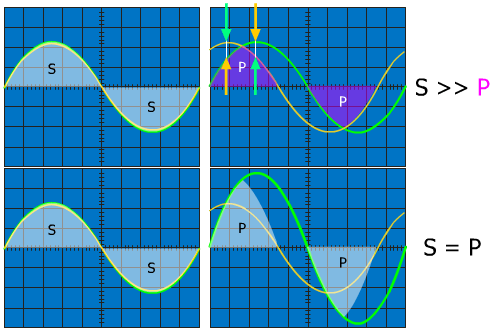 .
.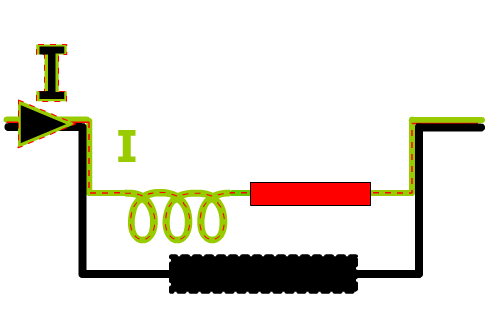
Le schéma ci-dessus reprend le précédent mais sans condensateur. On y voir bien que I générateur est supérieur car il fournit aussi le réactif...
P (W) / S (VA) = R (Ω) / Z (Ω) = Cosφ
Quand le cosφ peut être bon ou mauvais ?
- Les résistances chauffantes ont un cosφ ≃ 1 mais il est impossible de dépasser 1 !
- Les condensateurs présentent un cosφ = 0 : déphasage 90°
Pour les récepteurs :
- Un moteur à vide offre un très mauvais cosφ ≃ 0 car il ne fournit rien !
Il consomme essentiellement du réactif - Un moteur en charge à sa puissance nominale
a un cosφ tel qu'inscrit sur sa plaque signalétique (ex : 0.85) - Il en va de même que pour le moteur en ce qui concerne le transformateur
Conclusion en images, ce qui est fournitS en VA (Volt*Ampère) est fourni par le générateur, transportéS en VA est transporté et exploitéSeul P en Watt est exploité même si Q en VAR est nécessaire... :
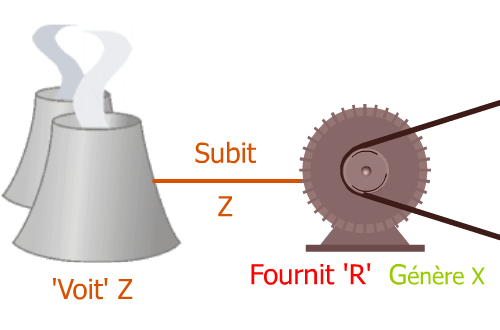

Reprenons le cos φ de notre exemple ≃ 0.3, avec une puissance non plus en Watts mais en kW pour mieux 'impacter' les esprits :
Soit un rapport ≃ 3 !
Comme la tension est fixe, c'est l'intensité qui subira cette augmentation !
Sans condensateurs on doit produire et transporter 4600 kW
Avec les condensateurs seulement 1800 kW !
Soit un rapport ≃ 3 !
Comme la tension est fixe, c'est l'intensité qui subira cette augmentation !
Donc des câbles de section ≃ 3 fois plus élevée, des pertes Joule ≃ 9 fois supérieures (I²), une masse de conducteurs plus élevée (piliers plus proches, plus solides...) et des protections électriques, elles aussi, 3 fois supérieures !
A retenir P = U × I × cosφ
P (W) = U × I × cos(φ)
P précise la puissance électrique active en Watt,
C'est celle qui est utile (puissance mécanique convertie sur un moteur)
S (VA) = U × I
S est la puissance fournie en Volt × Ampère par le générateur et transportée,
Elle détermine aussi la section des câbles et le calibre des protections
Q (VAR) = U × I . sin(φ)
Q, puissance réactive en Volt × Ampère réactif,
assure la création du champ magnétique tournant,
On peut la compenser avec des condensateurs car elle est taxée
NB : On dit souvent compensée pour le réactif généré par les condensateurs !
Invité, affichez le quiz :

Stage : INITELEC






